코딩을 하디보면 이 코드가 효율적인 코드인지 비효율적인 코드인지 고민을 하게 되는 순간이 오게 될것입니다.
그렇다면 효율적인 코드는 어떤것이며 어떤게 효율의 기준이 되는것일까요?
시간복잡도와 공간복잡도는 효율적인 코드의 기준점
어렵게 생각하지 마시고 한번 일상생활을 생각해 봅시다.
여러분이 살면서 ~~의 효율을 높여라 라는 말을 들어보셨을 겁니다.
알바를 하든, 작업을 하든, 공부를 하든 말이죠
이런 일들에서의 효율은 무엇을 말하는걸까요?
효율에는 두가지 종류가 있죠
일을 빨리 끝낼수 있는 시간에 대한 효율, 적은 자원을 투자하고 높은 결과를 이끌어 내는 자원에 대한 효율 이렇게 말입니다.
프로그래밍 세계에서의 효율 역시 현실세계의 효율과 의미가 같다고 보시면 됩니다.
시간복잡도
시간 복잡도는 일상생활에서의 일을 처리하는 시간과 같다고 보시면 됩니다.
어떤 코드를 실행하는데 얼마만큼의 시간이 걸리냐 라는 것이죠.
빅-오 표기법
시간복잡도를 계산할때는 빅-오 표기법을 많이 사용합니다.
예를들어 여러분이 주사위를 굴려서 3이라는 숫자가 나오게 하려고 합니다.
운이 좋다면 한번만에 3이 나올수 있지만 운이 좋지않다면 n번의 주사위를 굴려야 합니다.
이렇게 최악의 경우를 계산하는 방식을 빅-오(Big-O) 표기법 이라고 합니다.
빅오 표기법은 다음과 같습니다.

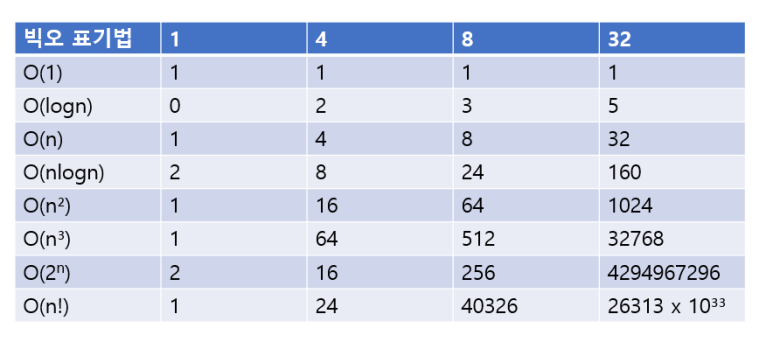
이곳에서 (n은 입력되는 데이터를 의미합니다)
다음으로 여러가지 시간복잡도를 가지는 알고리즘을 확인해보겠습니다.
O(1)의 시간복잡도를 가지는 알고리즘
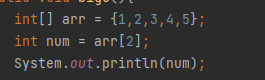
가장 빠른 O(1)의 시간복잡도를 가지는 알고리즘은 index로 배열의 element에 접근하는 것입니다.
O(n)의 시간복잡도를 가지는 알고리즘
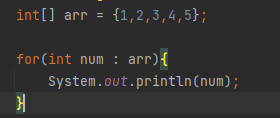
O(n)의 시간복잡도를 가지는 알고리즘은 1중 loop문을 사용하는 알고리즘입니다.
O(n²)의 시간복잡도를 가지는 알고리즘
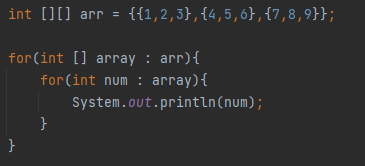
O(n²)의 시간 복잡도를 가지는 알고리즘은 2중 loop문을 사용하는 알고리즘입니다.
이를 통해 저희들이 알수있는건 중첩 loop문을 사용할때마다 n의지수가 하나씩 늘어난다는 것입니다.
당연히 중첩 loop문이 많이 이루어질수록 시간복잡도가 늘어나기 때문에 좋지 못한 알고리즘이 됩니다.
(O(n²)의 시간복잡도 까지는 괜찮으나 지수가 3제곱이 넘어가버리면 뭔가가 잘못되고 있는것...)
O(2ⁿ)의 시간복잡도를 가지는 알고리즘
그렇다면 가장 괴랄한 접근시간을 가진 O(2ⁿ)의 시간복잡도를 가진 알고리즘은 뭐가 있을까요?
https://blog.naver.com/cjy2103/222776932947
자바(Java) 이론 - 재귀함수 / 팩토리얼, 피보나치 수열
재귀함수? 대학에 들어가서 코딩을 하시거나 책을 읽다보시면 접하게 되시는 함수입니다. 재귀함수는 말그...
blog.naver.com
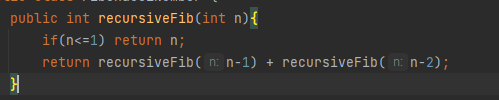
가장 유명한 알고리즘은 피보나치 수열입니다.
현업에서 재귀를 잘 안쓴다고 했던 이유가 바로 이런점 때문이죠..
공간복잡도
공간복잡도는 프로그램을 실행시킨 후 완료하는데 필요로 하는 자원의 공간을 말합니다.
(요즘은 워낙 메모리 용량이 넘쳐나서 옛날보다 별로 신경은 안쓰는것 같습니다.)
총공간 = 고정 공간 요구 + 가변 공간 요구로 나타내며 수식은 다음과 같습니다.
S(P) = c+Sp(n)
고정 공간은 입력과 출력의 횟수나 크기와 관계없는 공간의 요구(변수, 고정크기의 구조체, 상수, 코드저장공간)를 말합니다.
가변 공간은 특정 인스턴스에 의존하는 크기를 가진 구조와 변수들을 위해서 필요로 하는 공간, 함수가 순환 호출을 할 경우 요구되는 추가 공간.
즉 동적으로 필요한 공간을 말합니다.
공간 복잡도 예시

다시 위 재귀 함수를 보도록 하겠습니다.
피보나치 수열과 재귀 함수를 설명할때 제가 메모리에 어떤식으로 재귀 함수가 저장된다고 했었나요?

이런식으로 저장된다고 했었죠?
즉 n이 1이하가 될때까지 함수가 재귀적으로 호출되기 때문에 스택에는 n에서 1까지 모두 쌓입니다.
즉 O(n)의 공간복잡도를 가진다는 뜻이죠.
그렇다면 위의 피보나치 수열을 일반 loop문으로 구현하면 어떻게 될까요?

n의 값에 상관없이 스택에는
result, first, second, n, i 값만 저장이됩니다.
이때의 공간복잡도는 O(1) 입니다.
결론
시간복잡도는 얼마나 빠르게, 공간복잡도는 얼마나 적은 자원으로 알고리즘을 돌릴수 있느냐를 기준으로 좋은 알고리즘을 판별합니다.
즉 좋은 알고리즘은 시간도 적게걸리면서 자원도 덜먹는 알고리즘이라는것이죠
하지만 어느 법칙에서도 그렇듯... 모든것을 다 만족할수는 없습니다.
흔히 시간과 돈은 항상 반비례 한다고 말하잖습니까?
시간복잡도와 공간복잡도 역시 마찬가지입니다. 시간과 공간은 반비례 하기 때문에 요즘같이 메모리 용량이 늘어나 넉넉한 시대에는 공간복잡도 보다는 시간복잡도를 위주로 효율적인 알고리즘의 척도를 판단합니다.
'개발관련 > 용어' 카테고리의 다른 글
| 객체지향 프로그래밍이란? (0) | 2023.06.29 |
|---|---|
| 안정정렬, 불안정 정렬, 제자리 알고리즘 / Stable Sort, Unstable Sort, In-place Algorithm (0) | 2023.06.29 |
| 스펙트로그램(Spectrogram)? (0) | 2023.06.28 |
| 개발용어 관련 - 형상관리(Configuration Management) / CVS, SVN, Git (0) | 2023.06.28 |
| 개발 용어 관련 - Dry Code / Wet Code? (0) | 2023.06.27 |